How to factor as Factoring quadratic equations to find the roots of the given quadratic expressions is possible though expressing the equation as a product of its linear components. Algebra and quantitative ability both heavily rely on quadratic equations.
In this post, we will examine various approaches for factoring quadratic equations. The factorization approach can be used to solve these one-variable equations. We will also present a few instances with solutions to comprehend the various concepts better.
What Is a Factor?
A factor is a number that completely divides another number. To put it another way, adding two whole numbers results in a product. Then the numbers we are adding are factors of the product since they are divisible. Factors can be found using either division or multiplication rules.
Formulas for Factorization
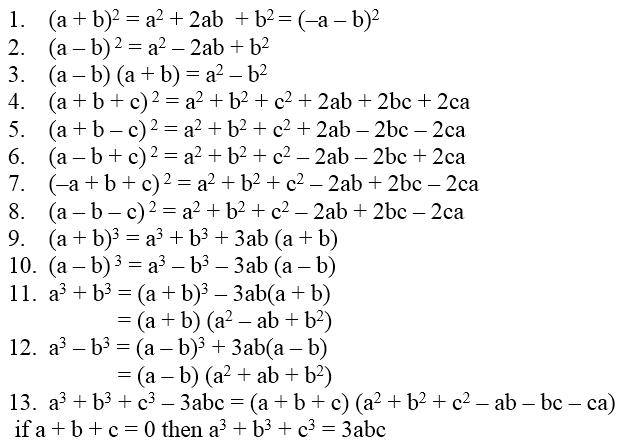
Factorization, commonly referred to as factoring, divides a big number into several smaller numbers. When we multiply these little integers, we will obtain the genuine or original number. Factorization ideas are often presented to pupils in Grade 6.
Factorization is one of the key techniques for reducing an algebraic or quadratic equation to a simple form. Therefore, one needs to be familiar with Factorisation Formulas to decompose the complicated equation.
This post will give you all the knowledge you want on various factorization formulas for polynomials, trigonometry, algebra, and quadratic equations.
First-order factorization
Finding factors for a given number, whether a prime or composite number, is a process known as factorization. The technique of obtaining the prime factors of a given composite number is known as prime factorization. In other words, the Prime Factorization Method only applies to Composite numbers. There are two ways to discover the number’s prime factors.
How to Double-Check Your Factoring
You may verify your newly factored equation by multiplying the terms of the factors using the FOIL order. That represents the first, outer, inner, and last terms. If you’ve done the math correctly, the outcome of your FOIL multiplication. It should be the initial, unfactored expression you begin with.
By putting the original phrase in a polynomial calculator, you may double-check your factoring by getting a list of factors. You can compare the outcome of our calculations. But bear in mind that, despite its usefulness for rapid spot-checks. This kind of calculator cannot replace how to factor algebraic equations on your own.
How to Factor Pyramid Math
Pyramid math is a unique method for teaching fundamental addition abilities by illustrating 10 boxes. Those piled in the shape of pyramid boxes’ numbers added to the top.
Another modification is multiplying the numbers at the bottom until you reach the result at the top. It can be made into an exercise. The factors are provided by going backward.
Draw a row of four contiguous, consecutive boxes to form a mathematical pyramid. Draw three more boxes immediately on top of these, then two more below that, and finally, one box on top of everything.
Put the finished item in the top box. The number must not be a prime number or the sum of two prime numbers for the pyramid to function. The two components of the product must also have a common element.
Using binomial factors
Binomials are two-term algebraic expressions. A binomial equation is factored in when it is reduced to its most basic form. You must divide the phrase into two simpler expressions enclosed in parenthesis to factor binomials:
A binomial must have two terms, and at least one must include a variable like x to be considered real. Whole numbers, negative numbers, decimals, and value exponents can all be included in binomials. Furthermore, it makes no difference if the first or second terms contain variables.
How to Factor Reducible Equations

A reducible equation may be easier to understand by “reducing” its terms to a more straightforward comparable equation. We are looking at a reducible equation where the unknown only makes up one side. But is additively or multiplicatively connected to another integer.
For the first time, we discover that the unknown appears on both sides of a reducible equation. The initial step in this scenario is to combine all the terms with the unknown on one side of the equation. It is necessary to leave all other terms on the opposite side of the equation.
It’s crucial to remember that all the words are connected additively. Meaning that adding or removing might transfer them to the other side, never by division or multiplication.
This happens when we want to change the coefficients of unknowns from one side to the other of the equation. We must do the last step of these equations.
Divide by the Common Factor
A polynomial multiplied by a common factor is shown in a reducible equation that we discover. In this instance, we must locate the product before proceeding, as in the previous example. Firstly, by removing the coefficient of the unknown. Secondly, by modifying the independent term from one side.
In this instance, the fact that each term in the equation has a denominator makes us first nervous and uncertain. We must formulate an analogous equation to simplify and decrease this equation. To simplify all the fractions, we must multiply both components of the equation by the same amount.
Algebraic Expression Factoring
Finding the factors of an algebraic expression, also known as locating two or more expressions. That product is the given expression, is the process of factorization. The factorization of algebraic expressions recognizes two or more expressions. Those products are the given expression.
A factor is a number that evenly divides the inputted number. It only represents a number as the product of two other integers. Similarly, algebraic expressions are written as a product of their components.
The main exception is that an algebraic statement here combines addition. Or subtraction with arithmetic operations like numbers and variables.
Conclusion
For various reasons, an algebraic term or the full algebraic expression may be rewritten as the result of two or more multiplying expressions. In algebraic form, each multiplying statement denotes a quantity and is known as a factor.
In mathematics, it is known as an algebraic factor. An algebraic factor is a quantity in an algebraic form that multiplies at least one quantity in an expression’s term.























































