Binary to hexadecimal conversion is another process that happens in the number system. Binary, octal, decimal, and hexadecimal are four types of number systems used in mathematics.
Each form may be converted to another type of number system using the conversion table or the conversion process. Let’s examine the various procedures for converting binary integers to hexadecimal numbers. And work through a few examples to gain a better grasp.
What is Binary to Hexadecimal Conversion?
Translating binary numbers into hexa values is known as binary to hexadecimal conversion. Hexadecimal has a base number of 16, whereas binary digits have a base number of 2. With the aid of the base numbers, binary is converted to hexa.
There are several ways to perform the conversion. The first is changing the binary representation into a decimal number and then a hexadecimal number. The second method involves utilizing a table that converts binary to hexadecimal.
System of Binary Numbers
Computers that are particularly useful for engineers, networking experts, and computer specialists typically employ binary numbers. One of the simplest number systems is the binary system, which uses the digits 0 and 1 and the base number 2.
Bits are the digits 0 and 1, and a byte consists of 8 bits. Other numbers, such as 2,3,4,5, and so on, are not included in the binary number system.
System of Hexadecimal Numbers
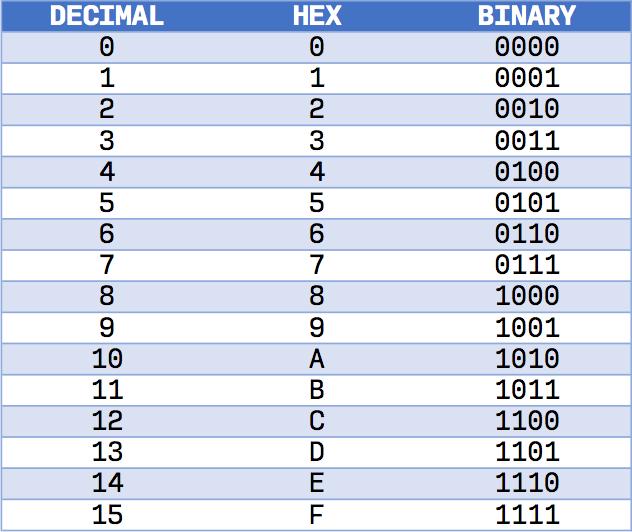
The hexadecimal number system is a positional numeral system. It employs the base number of 16 together with sixteen digits/alphabets: 0, 1, 2, 3, 4, 5, 6, 7, 8, and A, B, C, D, E, F.
Each digit in the hexadecimal number system represents the base’s power. A-F of the hexadecimal system corresponds to the numbers 10-15 of the decimal number system, respectively.
How to convert Binary to Hexadecimal?
A significant component of mathematics is number systems. The binary, hexa, and binary to hexadecimal number systems are discussed in this article. Various mathematics and computer science branches employ the number system and its conversions.
It is further mentioned that converting from binary to decimal is fairly simple. The binary number system uses the base-2 notation to denote numbers. Only 0s and 1s represent numbers in the binary number system. Bits or binary digits are the names for the digits used in the binary number system.
Steps to Convert Binary to Hexadecimal
We must utilize the base numbers 2 for binary and 16 for hexadecimal to convert binary to hexadecimal values. One hexadecimal integer equals four binary numbers in the binary-to-hexa conversion table.
It is the initial method used in the conversion process. The second way entails changing the hexa number from a decimal to a binary format.
Method 1
The conversion table is among the simplest and quickest ways to get from binary to hexadecimal. Since hexa numbers are also positional number systems, binary numbers only include the digits 0 and 1. Every four bits are equal to one hexadecimal number, including the letters A through F.
Method 2
Binary integers may change into hexa numbers without employing a conversion table. Before transforming into a hexadecimal number, binary numbers are translated to decimal values. A decimal number’s base number is 10.
By multiplying each digit of the binary number by the power of either 1 or 0 and the corresponding power of 2. The binary number may transform into a decimal number. Additionally, we divide the number 16 until the quotient equals zero to convert from decimal to hexadecimal.
Convert Binary to Hexadecimal With Decimal Point
We employ a technique similar to the previous section to convert binary to hexadecimal with a decimal point. The conversion table is used to change binary integers into hexadecimal numerals.
When a binary number has a decimal point, the fractional portion is also there and is thought of as coming after the decimal point—the location of the numerals unaffected by the decimal point during the conversion.
Why is it important?
The base-16 numbers, which include hexadecimal numerals, are currently the biggest. The hexadecimal numerals go from 0 to 9 and comprise A, B, C, D, E, and F.
Experts think of hexadecimal numbers as the more sophisticated form of binary numbers. Hexadecimal numerals have also begun to replace zeros and ones in many contemporary organizations.
Additionally, hexadecimal numerals utilize to increase a website’s security. A common practice among developers is to convert the decimal number to hexadecimal before saving it to the database.
To present it to the users, they first convert the number from hexadecimal to decimal. Because embedded systems frequently require decimal numbers, this translation is helpful for them.
Humans can read and understand decimal numbers rather simply. Decimal numbers can also pose a hazard to people. Because of this, hexadecimal to decimal conversion is crucial.
Apart from that, the hexadecimal number has the following advantages and disadvantages. Hexadecimal numerals are extremely compact, which is their main benefit.
Because it is a base-16 integer, it may be represented with the fewest possible characters. A decimal is a base-10 number with around 16 characters, making it a base-16 number. Binary only uses zeros and ones; therefore, representing a number in binary requires eight times as many integers as in hexadecimal.
Replace zero
Due to this benefit, hex numbers have begun to replace zeros and ones in many major enterprises. In addition, hex numbers are simple for computer processors and other electrical systems to process, which speeds up their operation. Therefore, hex numerals are preferred above all other numbers by businesses that value speed in a processor.
Additionally, the MAC address uses hexadecimal integers to provide a distinct ID for each electronic device on the network. Additionally, sophisticated computer and electronic systems require hex digits.
Many technical individuals see hexadecimal numbers as the future of the numbering system. Acquiring the necessary expertise to pursue a career in this area is vital.
Conclusion
Computers utilize binary to hexadecimal to calculate and display data. Computers utilize binary because there are only two states on and off binary. Computers are built with binary, and thinking in binary may also be useful for solving logical issues. As a result, it provides a thorough explanation of hexadecimal numerals.
Also read: Best Ways To Convert Millilitres To Grams























































