In physics, often students get confused between terms that seem similar yet are different from one another. It is prevalent to get confused; many students often get confused between velocity and speed, distance and displacement. But, the two terms have a significant difference between them.
Let us discuss the Distance and Displacement Differences which will help us to understand these terms in a better way and how these terms are used to solve problems.
The distinction between Distance and Displacement
Here we will discuss the primary distinction between distance and displacement.
| SL NO | POINT OF DIFFERENCE | DISTANCE | DISPLACEMENT |
| 1. | Definition | The total length of paths between two consecutive points is known as distance | The direct length between two consecutive points, when measured along the shortest path, is known as displacement |
| 2. | Quantity | It is a scalar quantity as it only depends upon the magnitude of the path and not the direction. | It is a vector quantity as it depends upon both direction and magnitude. |
| 3. | Denotation | d | s |
| 4. | Formula | Speed x Time | Velocity x Time |
| 5. | Path Dependence | It depends upon the path as it can change with the path taken to travel. | It does not depend upon the path chosen, but it depends upon the initial and final position of the object. |
| 6. | Direction Consideration | The direction is not considered to calculate distance. | Direction is taken into consideration while calculating displacement. |
| 7. | Route Information | It gives complete information about routine taken between the consecutive two points. | As it depends upon the initial and final position, hence route information is not required. |
These points will help you to distinguish between distance and displacement and not confuse these two terms.
Let us discuss some simple problems that will help you to understand how distance and displacement work.
Problems
1. A vehicles’ speedometer reads 10,500 km at the start of a trip and 10,700 km at the end. Determine distance and displacement.
Ans: The distance of the car = (10700 – 10500) km = 200 km
The displacement of the car = 0 km ( as the car returns to the starting point)
2. A person walks along the path of a rectangle from point P to point R, as shown in the below figure.
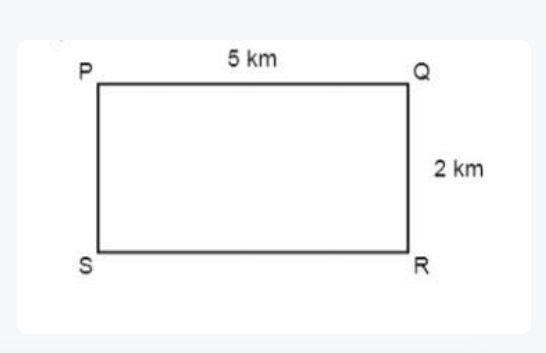
a) Find the distance travelled by the person.
b) Find out the magnitude of the displacement of the person.
Ans: The distance given for PQ = 5km
The distance for QR = 2 km
- The distance travelled by the person = PQ + QR
= 5 + 2 = 7 km
- We know that the magnitude of displacement is the shortest distance between P and R points, respectively. It is the diagonal of PR, and it can be calculated using the Pythagoras theorem.
By Pythagoras Theorem,
PR2 = PQ2 + QR2
Displacement = PR
= √ (PQ)2 + (QR)2
= √ (5)2 + (2)2
= √29
= 5.385 km
3. A boat sailing through a river moves eastward for 5 km, then crosses the river by moving 3 km southward. On reaching the other side, it moved westward through 1 km and reached the jetty. Find the distance covered and displacement of the boat.
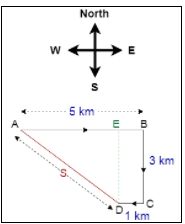
Ans: AB = 5 km
ED = BC = 3 km
CD = 1 km
∴ AE = 5 km – 1 km = 4 km
Distance covered = AB + BC + CD
= 5km + 3km + 1 km
= 9 km
Displacement, s = AD
= √ (AE)2 + (ED)2
= √ (4)2 + (3)2
= √ (25)
= 5 km
Hence, the distance covered by the boat is 9 km, and the displacement is 5 km.
4. A motorcycle rides from point P to Q to R to S and finally to P in a circular path, as shown in the below figure. Find
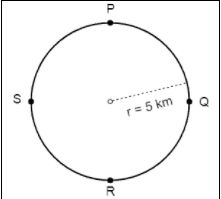
a) the distance travelled by motorcycle.
b) the displacement.
Ans: The given radius, r = 5 km
a) Here, the distance travelled by motorcycle
= circumference of the circle
(∵ the motorcycle moves one complete rotation)
= 2πr
= 2 × 3.14 × 5
= 31.4 km
b) Here, the initial point is P, and the final point is also P. Therefore, there will be no change in position, and hence the displacement is equal to zero.
5. An object moves along the grid through the points A, B, C, D, E, and F, as shown below.
a) Find the distance covered by the moving object.
b) Find the magnitude of the displacement of the object.
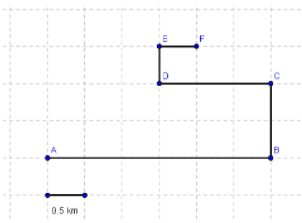
Ans: a) Distance = AB + BC + CD + DE + EF = 3 + 1 + 1.5 + 0.5 + 0.5 = 6.5 km
b) Initial point is A, and the final point is F Hence, the displacement’s magnitude is equal to the distance AF, which is calculated by applying Pythagoras theorem to the triangle AHF as shown in the figure.
AF2 = AH2 + HF2 = (0.5 x 4)2 + (0.5 x 3)2
AF = √(4 + 2.25) = √6.25
the magnitude of displacement = AF = 2.5 km
New Informations
Besides comparing Distance and Displacement, there are also many similarities between these two components. Some of the similarities between Distance and Displacement are as follows:
- The S.I unit of both displacement and distance is the same. It is meter (m).
- Reference points are required to measure both of these components.
- Both have the same dimension.
- If the body travels in a straight line, then both displacement and distance will be the same.
Important Conversions
The basic conversions are taught in your mathematics class like a meter to the centimetre, kilometre to meter etc. Here are some more conversions that you will need in your studies.
- 1 Inch = 2.54 centimetres
- 1 ft = 30.48 centimetres
- 1m = 100 centimetres
- 1 N (newton) = 105 dynes
- 1 J (joule) = 107 ergs
- 1 P (pascal) = 10 Ba
Conclusion
All these conversions are important, and you will need them while solving problems. After you have learnt about the major difference between distance and displacement and how to solve problems, you need to practise some problems yourself to clear your concepts.
Try some difficult questions given to you. You will face questions about Distance and Displacement all the time. So, you need to clear your doubts.
Also read: How To Calculate Miles To KM





